素数探索はじめました

筆者が VPS（Virtual Private Server）を利用するようになって，半年以上が経ちました．しかし，個人サイトをホストする他は，ごく稀に実行に時間のかかるプログラムを動かす目的でしか利用していなかったため，利用開始以来の平均 CPU 使用率がほぼ0%といえる状態が続いているのが実情でした．

それではあまりにもったいないということで，先月から GIMPS という素数の探索を目的とする分散コンピューティングプロジェクトに参加し，筆者の利用していない「余った」リソースで，現代科学の発展に貢献しています．

本稿では，まず分散コンピューティングの概念や GIMPS というプロジェクトについて簡単に解説し，その上で VPS を用いて具体的にどのようにすれば GIMPS に参加できるのかという知見を共有したいと思います．

分散コンピューティング
GIMPS とは
- 数学的背景とアルゴリズム
  - メルセンヌ素数
  - リュカ＝レーマーテスト
- これまでの実績
GIMPS に参加する
参考文献

分散コンピューティング

コンピュータの性能は日進月歩していますが，それでも1台のコンピュータの計算能力には限界があります．また，スパコンのように巨大で貴重な計算資源は，世界中の研究者やそれに類する人々が様々な用途で使用を希望するもので，1つの目的のために専有することは困難です（少なくとも非常に大きなコストがかかります）．

そこで，世界中の個人や団体の所有するマシンの，使用されていないリソースを活用して大規模なプロジェクトの計算資源として活用しよう，というのが分散コンピューティングの基本的な発想です．すなわち分散コンピューティングとは，ネットワークを介して複数のコンピュータを接続・連携させ，1台の高性能なコンピュータを仮想的に構築する技術のことをいいます．

現在ではインターネットおよび性能の良いパソコンが広く普及していることもあり，誰でも簡単に参加することのできる分散コンピューティングプロジェクトが多く存在します．このような分散コンピューティングプロジェクトには

Einstein@Home：LIGO 重力波検出器の観測データから重力波を検出
Folding@home：タンパク質の折りたたみ構造を解析
M4 Project：第二次世界大戦中に傍受されたナチスの未解読暗号を解読
SETI@home：地球外からの信号を解析し，地球外生命体を探索
∞Eyes：いくつかの検索エンジンの検索結果を比較し，グーグル八分を発見 *1

などがあり，学術研究に関するものから一見すると「ネタ」のように思えるものまで様々です．

こうしたプロジェクトの多くには，管理サーバからタスクを取得して計算を実行し，その結果をサーバに報告するという一連の作業を自動的に行うクライアントプログラムが用意されています．したがって参加者は，自分がリソースとして提供したいマシンに専用のクライアントプログラムをインストールし，これを起動しておくだけで，簡単に分散コンピューティングに参画することが可能です．

GIMPS とは

自身および1以外に約数をもたないような2以上の整数を素数と呼ぶことは，皆さんご存知の通りでしょう．また，素数は数々の摩訶不思議な性質をもち，関連する数学上の未解決問題が多いこともよく知られた有名な事実だと思います．「素数は無限に存在する」という命題は背理法により容易に示すことができますが *2 ，素数の出現パターンは一見するとランダムであり，人類は未だに明確な法則性を導くことに成功していません．そのため巨大な素数を見つけ出すことは，容易なことではないのです．

一方で，素数は現代の暗号理論（特に公開鍵暗号関連）で中核をなす重要概念であり，現在も数多くの数学者が素数に関する問題を解くべく必死の研究を続けています．人類がまだ知らない巨大な素数を見つけ出すことは，こうした研究を後押しする方法の1つです．

本稿で解説する GIMPS（Great Internet Mersenne Prime Search）は，メルセンヌ素数と呼ばれるある特殊な形をした素数を探索する，実績ある分散コンピューティングプロジェクトです．

数学的背景とアルゴリズム

メルセンヌ素数

2のべき乗から1を減じた数，すなわち $2^n-1$ （ $n$ は自然数）の形で表される自然数をメルセンヌ数といい， $M_n$ のように表記します．

$\displaystyle\quad \{M_n\} = 1, 3, 7, 15, 31, 63, 127, 255, 511,\ldots$

さらに $M_n$ が素数のとき，これをメルセンヌ素数といいます．メルセンヌ素数は2016年8月現在49個が知られていますが *3 ，無限に存在するのか否かはわかっていません．

一方，メルセンヌ素数に関しては「 $M_n$ がメルセンヌ素数ならば， $n$ は素数である」という定理が知られています（逆は成り立ちません）．これは， $n$ が $n=pq$ （ $p,q$ は自然数）と表される合成数のとき

$\displaystyle\quad 2^n-1 = (2^p-1)(2^{pq-p}+\dots+2^{3p}+2^{2p}+2^p+1)$

が成り立って， $2^p-1$ という因数をもつことから（対偶が成り立つので）直ちに示されます．

リュカ＝レーマーテスト

さて，一般にある程度以上大きな自然数について，その数が素数であるかどうか判定することは簡単にはできません．しかし，メルセンヌ数に関してはリュカ＝レーマーテストという比較的単純で効率のよい素数判定法が知られています．この判定法はフランスの数学者エデュアール・リュカ *4 が考案し，1930年頃にデリック・ヘンリー・レーマーが改良を加えたものです．

リュカ＝レーマーテストでは，まず初項 $S_1=4$ ，漸化式 $S_{n+1}={S_n}^2-2$ で与えられる数列

$\displaystyle\quad \{S_n\} = 4, 14, 194, 37634, \ldots$

を定義します．このとき「 $M_{2n+1}$ で $S_{2n}$ を割り切れる」ことと「 $M_{2n+1}$ が素数である」ことは同値になります *5 ． $S_n$ の値は急激に大きくなっていきますが，素数判定を行うためには実際の $S_n$ を計算する必要はなく，合同式を用いた剰余計算を行うだけで十分であるため，コンピュータを用いて効率的に判定を行うことが可能です．

GIMPS では，このリュカ＝レーマーテストを用いて巨大なメルセンヌ素数の探索を行っています．

これまでの実績

GIMPS は1996年1月にジョージ・ウォルトマンがリュカ＝レーマーテストによってメルセンヌ数の素数判定を高速に行うプログラムを公開したことに端を発して始動しました．プロジェクトの発足当初は E-mail によって素数判定を行うメルセンヌ数を依頼するなどといった原始的な手法が用いられましたが，プロジェクトの規模が拡大するのに伴って，そのシステムが改良されてきたようです．GIMPS は，現在では1秒間に2兆回の演算を1日中実行することのできるエントロピア社の PrimeNet システムを中心に，日夜を問わず素数の探索を行っています．

GIMPS の最初の成果はプロジェクト発足と同じ1996年の11月13日に挙げられました．その後も GIMPS はいくつもの新しいメルセンヌ素数を発見し，その数は2016年8月現在15個にのぼっています．

GIMPS に参加する

GIMPS のようなプロジェクトに参加するのは一見すると敷居が高いようにも思われますが，実はそれほど難しいことではありません．本稿でこれから示す手順にしたがってクライアントソフトをダウンロード・インストールし，起動させておくだけで，誰でも簡単にメルセンヌ素数探索を始められます．これらの作業を行うのには1時間も必要ないでしょう．

プログラムを走らせるマシンを1年365日24時間起動させっぱなしにすればその分の電気代はかかるわけですが，元々月額制で借りている VPS を用いて参加する場合は特に何の負担が増えるわけでもなく現代科学の発展に貢献することができます．そればかりか，運良く自身のマシンでメルセンヌ素数を発見した場合には懸賞金がもらえる可能性もゼロではありません．

PrimeNet アカウントの作成

GIMPS に参加するには，まず PrimeNet（mersenne.org）にログインするためのアカウントを作成することをおすすめします．このアカウント取得は必須ではありませんが，アカウントがないと PrimeNet で CPU の稼働状況や自身の貢献度を確認することができません．

PrimeNet のアカウント作成は非常に簡単で新規アカウント作成ページで希望するログイン ID とパスワードを入力し，画面下部の “Create Account” ボタンを押すだけです．公開名，E-mail アドレス，ウェブサイト URL は任意で登録することができます（これらの設定はあとから変更可能です）．

クライアントソフトの使い方

本節では GIMPS のクライアントソフト Prime95（別名：mprime）を VPS 上でどのようにインストール・実行すればいいのかについて具体的に解説します．ここで，VPS には SSH 等でシェルログインしていることを想定しています．OS は Linux であれば，何であれ操作はほぼ同様と思われますが，筆者は次の環境で動作確認を行いました．

$ cat /etc/redhat-release
CentOS Linux release 7.2.1511 (Core)
$ uname -svrmo
Linux 3.10.0-327.10.1.el7.x86_64 #1 SMP Tue Feb 16 17:03:50 UTC 2016 x86_64 GNU/Linux

インストール

まず，Prime95 のダウンロードページにアクセスし，使用したいマシンに搭載された OS に適したプログラムの置かれたリンクを調べます．その上で，該当するアーカイブファイルをダウンロード・解凍します．例えば，2016年8月現在最新版の 64bit Linux 用プログラムをインストールする場合は，次のようにするのが最も手っ取り早いでしょう．

$ wget http://www.mersenne.org/ftp_root/gimps/p95v289.linux64.tar.gz
$ tar xvzf p95v289.linux64.tar.gz

すると，カレントディレクトリに mprime という実行ファイルと，いくつかのテキストファイル（*.txt）が現れます．前者がプログラム本体で，後者がそのドキュメント類です．./mprime を -v オプション付きで実行し

$ ./mprime -v
Mersenne Prime Test Program: Linux64,Prime95,v28.9,build 2

のようにバージョン番号が表示されれば，インストールは成功しています．

セットアップ

それでは，いよいよ Prime95 を起動してみましょう．今度は ./mprime をオプションなしで実行します．すると，初回起動時には次のようなメッセージが表示されるはずです．

$ ./mprime

Welcome to GIMPS, the hunt for huge prime numbers.  You will be asked a
few simple questions and then the program will contact the primenet server
to get some work for your computer.  Good luck!

Attention OVERCLOCKERS!!  Mprime has gained a reputation as a useful
stress testing tool for people that enjoy pushing their hardware to the
limit.  You are more than welcome to use this software for that purpose.
Please select the stress testing choice below to avoid interfering with
the PrimeNet server.  Use the Options/Torture Test menu choice for your
stress tests.  Also, read the stress.txt file.

If you want to both join GIMPS and run stress tests, then Join GIMPS and
answer the questions.  After the server gets some work for you, stop
mprime, then run mprime -m and choose Options/Torture Test.

そして，その下にセットアップのための質問が表示され，その回答の入力待ち状態になります．

Join Gimps? (Y=Yes, N=Just stress testing) (Y):

最初の質問は「GIMPS に参加するか，単にストレステストのみを行うか」という質問です *6 ．本稿では GIMPS に参加することを目的としていますから，コロンに続けて Y を入力，改行します．なお，コロン直前のカッコ内には「現在の設定値」（初回起動の場合はデフォルト値）が表示されており，何も入力せずに改行をした場合にはその値が維持されます．

Use PrimeNet to get work and report results (Y):

次は「PrimeNet を利用するか」という質問が来ますが，GIMPS に貢献するためにはここも Y と答えます．

GIMPS への参加を表明すると，今度は PrimeNet アカウントを入力するよう求められます．先述した手順でアカウントを作成済みの方は，ここで作成したアカウントの ID を入力します．この ID の登録は必須ではありませんが（登録しない場合は空欄のまま改行します），登録をしないと PrimeNet での貢献度の確認をすることはできません（詳細後述）．

You must first create your user ID at mersenne.org or leave user ID blank
to run anonymously.  See the readme.txt file for details.
Optional user ID: 
Optional computer name: 
Computer uses a dial-up connection to the Internet (N): 
Optional proxy host name: 

Accept the answers above? (Y):

さらにコンピュータ名やプロキシホスト名もオプションで登録することができます．特に登録したくない場合は空欄のままで大丈夫です．

Hours per day this program will run (24):

続いて1日にプログラムを稼働させておきたい時間数を聞かれます．ここは，各自の都合に合わせて適当に設定すればいいでしょう．筆者は働き者なので24時間稼働させています．

Please see the readme.txt file for important
information on the P-1/ECM stage 2 memory settings.

Daytime P-1/ECM stage 2 memory in MB (8): 
Nighttime P-1/ECM stage 2 memory in MB (8): 

Accept the answers above? (Y):

今度はプログラムに使用を許可するメモリ量を，日中と夜間に分けて 8〜984MB の間で指定します．

そう言われても，どういう値を指定したものか迷うところですが，詳しいことは上のメッセージ中にもある通り readme.txt に記述されています．ただ，Prime95 は稼働時間の 98% は 8MB 以下のメモリしか必要とせず，実際のところ 8MB しかメモリを使用できなくても問題なく動作するようなので，ひとまず初期設定のままにしておいても良いようです．

Number of workers to run (1):

上の質問の意味は筆者もよくわかっていないのですが，同時進行させるタスクの数を指定するのでしょうか．規定値が 1 なのでそのままにしておけばいいと思います．

Pick a priority between 1 and 10 where 1 is the lowest priority and 10 is
the highest.  It is strongly recommended that you use the default priority
of 1.  Your throughput will probably not improve by using a higher
priority.  The only time you should raise the priority is when another
process, such as a screen saver, is stealing CPU cycles from this program.
Priority (1):

説明が長いですが，Prime95 の実行優先度を指定します．筆者の場合は Prime95 は VPS が暇しているとき（他の一切のプログラムが使っていないリソースで）稼働していて欲しいので初期設定のまま 1 としています．

Use the following values to select a work type:
  0 - Whatever makes the most sense
  2 - Trial factoring
  100 - First time primality tests
  101 - Double-checking
  102 - World record primality tests
  4 - P-1 factoring
  104 - 100 million digit primality tests
  1 - Trial factoring to low limits
  5 - ECM on small Mersenne numbers
  6 - ECM on Fermat numbers

Type of work to get (0):

これまで Prime95 の計算内容としてはリュカ＝レーマーテストしか紹介してきませんでしたが，実際には Prime95 ではリュカ＝レーマーテストを行う前の絞込みなどさまざまな計算を行っています．また，分散コンピューティングの弱点として「参加者が配布プログラムを改造するなどして，正しくない結果を報告してくる」リスクがあることから，GIMPS では判定演算のダブルチェックも実施しているようです．

上の質問項目は，そうした種々のタスクのうちのどれを引き受けたいかを番号で指定するものです．0 を指定すれば割り振られるタスクをサーバ側に一任することもできます．

CPU affinity (1-2=specific CPU, 99=any CPU, 100=smart assignment) (100): 
CPUs to use (multithreading) (2):

とうとうこの2つが最後の質問です．

いずれも CPU の使い方に関する設定のようですが，ハードウェアには詳しくないこともあり，「CPU の親和性」などと言われてもその意味すらよくわかりません．とりあえず 100=smart assignment を指定しておくと良しなに取り計らってくれそうなので，そのように指定しておけば大丈夫そうです．

使用する CPU の数も VPS の場合どうなっているのかよくわかりませんが，筆者が借りている ConoHa の VPS は2コアのように振舞っているようなので，これも初期設定のまま 2 としています．

さて，セットアップが終わると次のような「メインメニュー」と呼ばれる選択肢が表示されます．

              Main Menu

         1.  Test/Primenet
         2.  Test/Worker threads
         3.  Test/Status
         4.  Test/Continue
         5.  Test/Exit
         6.  Advanced/Test
         7.  Advanced/Time
         8.  Advanced/P-1
         9.  Advanced/ECM
        10.  Advanced/Manual Communication
        11.  Advanced/Unreserve Exponent
        12.  Advanced/Quit Gimps
        13.  Options/CPU
        14.  Options/Preferences
        15.  Options/Torture Test
        16.  Options/Benchmark
        17.  Help/About
        18.  Help/About PrimeNet Server
Your choice:

メニューを見て興味のある項目を選択してもらってももちろん構いませんが，ここでは早速実際の素数探索を開始するために少し特殊な方法でプログラムを起動し直したいので，一旦 “5. Test/Exit” を選んで Prime95 を終了させることにします．

なお，このメインメニューは ./mprime を -m オプション付きで実行すればいつでも開くことが可能です．

$ ./mprime -m

計算の実行

実際に VPS 上で素数探索の計算を開始する場合には，様々な点に注意しなければなりません．具体的には

ログアウトしても（SSH 接続を切っても）実行され続けるようにする
なるべく詳細なログをファイルに出力する
実行中の Prime95 に対して意図せぬ入力が発生しないようにする
Prime95 の起動中でも他の作業を行えるよう，バックグラウンドで実行する

ことが望ましいです．これらの条件を満たすように Prime95 を実行するコマンドを以下に示します．

$ nohup ./mprime -d >> mprime.log 2>&1 < /dev/null &

まず SSH 接続を切ってログアウトした後も計算を続行できるように nohup コマンドを使用しています．その上で ./mprime をなるべく詳細なログを出力する -d オプション付きで実行しているというところまでが基本的な構造です．

さらに，後続の >> mprime.log 2>&1 の部分で標準出力および標準エラー出力をすべて mprime.log ファイルに追記モードでリダイレクトし *7 ，一方で < /dev/null により余計な入力を受け取らないようにします．そして，末尾に & を付けることで処理をすべてバックグラウンドで行うように指定すれば上記実行文の完成です．

なお，この方法で起動した Prime95 を終了させる場合は，kill/killall コマンド等を使用してください．

$ killall mprime

実行状況の確認

ログとステータス

さきほど示した計算開始コマンドでは mprime 実行ファイルがあるディレクトリ内の mprime.log ファイルに出力されます．したがって，tail コマンド等でこのログファイルを見れば，計算の進行状況を知ることができます．

以下に，参考のため筆者の mprime.log から $M_{76547621}$ の（1回目の）リュカ＝レーマーテストを行ったことを記録する部分を抜き出しておきます．

[Work thread Aug 1 05:53] Setting affinity to run helper thread 1 on any logical CPU.
[Work thread Aug 1 05:53] Starting primality test of M76547621 using FMA3 FFT length 4M, Pass1=1K, Pass2=4K, 2 threads
[Comm thread Aug 1 05:53] PrimeNet success code with additional info:
[Comm thread Aug 1 05:53] CPU credit is 214.8152 GHz-days.
[Comm thread Aug 1 05:53] Done communicating with server.
[Work thread Aug 1 06:16] Iteration: 100000 / 76547621 [0.13%], ms/iter: 13.284, ETA: 11d 18:05
[Work thread Aug 1 06:38] Iteration: 200000 / 76547621 [0.26%], ms/iter: 13.317, ETA: 11d 18:24
[Work thread Aug 1 07:00] Iteration: 300000 / 76547621 [0.39%], ms/iter: 13.314, ETA: 11d 17:58

（中略）

[Work thread Aug 13 03:59] Iteration: 76500000 / 76547621 [99.93%], ms/iter: 13.651, ETA: 00:10:50
[Work thread Aug 13 04:10] M76547621 is not prime. Res64: FAB0EDBE6E8B1A46. We8: 24DDDC53,6766791,00000000
[Comm thread Aug 13 04:10] Sending result to server: UID: Watson_DNA/Watson-VPS, M76547621 is not prime. Res64: FAB0EDBE6E8B1A46. We8: 24DDDC53,6766791,00000000, AID: 6179303CD2F848D8E2A82C8941FACC8D

このログの下から2行目を見ると， $M_{76547621}$ は残念ながら素数ではなかったということがわかります．なお，ある時刻における反復回数の記録（Iteration: から始まる行）の出力頻度は，メインメニューの “14. Options/Preferences” から変更することができます．

また，./mprime を -s オプション付きで実行することによりステータスを確認することも可能です *8 ．

$ ./mprime -s
Below is a report on the work you have queued and any expected completion dates.
M70920893, Lucas-Lehmer test, Sat Sep  3 22:08 2016
The chance that the exponent you are testing will yield a Mersenne prime is about 1 in 531553.

上記の例では Prime95 は $M_{70920893}$ についてリュカ＝レーマーテストを行っていて，これが2016年9月3日（土）の22:08に終了する見込みであることがわかります．さらに，このステータス表示の面白いのは，最終行で現在判定を行っている数がメルセンヌ素数である確率を表示してくれるところです．先の出力によれば $M_{70920893}$ はおよそ53万分の1の確率でメルセンヌ素数であるようです．9月3日に結果が出るのが楽しみになりますね．

リソースの使用状況

バックグラウンドで Prime95 を実行していると，本当に計算が行われているのどうかはただコンソールを眺めているだけではわかりません．最も簡単にその実行状況を調べるのであれば，ps コマンドを使うといいでしょう．

$ ps u $(pgrep "mprime")

さらに，筆者が利用している VPS サービス ConoHa では Web システムを通して，リソースの使用状況をグラフィカルに確認することも可能です *9 ．

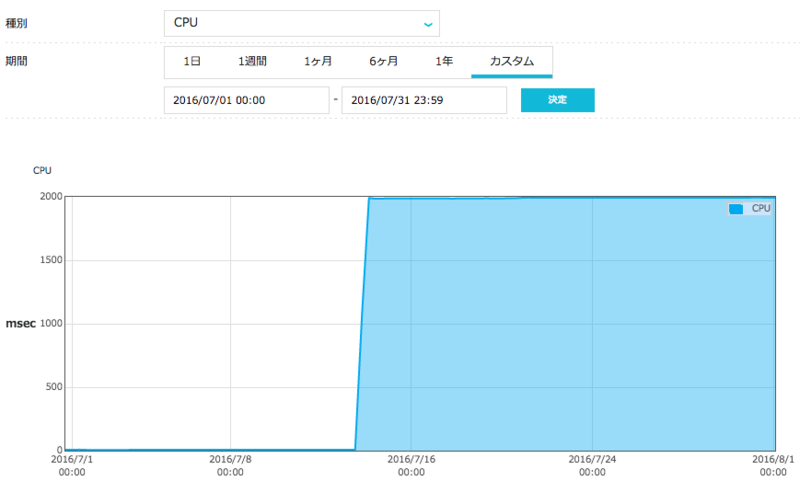
筆者の VPS における CPU 使用率の遷移

上のグラフを見れば，今までずっと無駄になっていたリソースが GIMPS に参加することによって一気にフル活用されるようになったことがひと目で分かります．

PrimeNet で貢献度を確認する

PrimeNet のステータスページでは，誰でも GIMPS プロジェクト全体の進行状況を確認することができます．さらに，GIMPS の参加者で先ほど作成方法を説明した PrimeNet アカウントの保持者は，所有アカウントのサマリーページにて自分の貢献状況を確認することも可能です．ただし，起動中のプログラムが PrimeNet のサーバと連絡をとるのは24時間に1度であり，また少なくとも1つのタスクを完了しないと何も表示されないため，最初の貢献状況がアカウントのサマリーページに反映されるまでには少し時間がかかります．

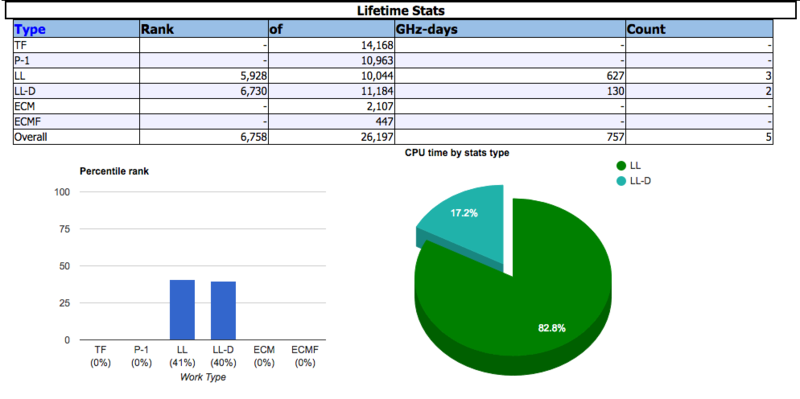
筆者の PrimeNet アカウントのサマリーページ

PrimeNet ではこのように，自分の貢献度を図表にしてわかりやすく表示してくれるので（実際はプログラムを起動させているというだけでも）しっかり素数探索に参加できている気がしてくるのが素晴らしいです．同時に，このページを確認することで自分の走らせているプログラムの計算結果が正しく PrimeNet 側に伝達されていることも確認できるので，次に GIMPS がメルセンヌ素数を発見した暁には「私もその発見にいくらか貢献した」と胸を張って言うことができそうです．